TVAR ZEMĚ A REFERENČNÍ PLOCHY
Povrch Země je v důsledku dlouhého historického vývoje velmi členitý a neustále podléhá dalším změnám (slapové působení, eroze …), proto by bylo na takové ploše nemožné určit přesnou polohu jakéhokoliv místa.
Tvar zemského tělesa se pro matematické výpočty idealizuje a nahrazuje nejčastěji geoidem a rotačním elipsoidem, pro širokou veřejnost pak koulí.
Geoid je fyzikálně definované těleso, které je vzhledem k atmosféře vymezeno střední hladinou oceánů a moří.Geoidem kopírujeme skutečný tvar Země.

- obrázek znázorňuje průběh geoidu a elipsoidu na povrchu Země
Pro vědecké účely je složitý a pro výpočty nepraktický,proto je geoid nahrazován rotačním elipsoidem.
Rotační elipsoid, který se alespoň částí přimyká ke geoidu se nazývá referenční elipsoid. Plocha referenčního elipsoidu se označuje jako referenční plocha.
Mezi nejznámější vypočtené referenční elipsoidy patří: Besselův elipsoid, Hayfordův elipsoid, Krasovského elipsoid, Elipsoid IAG 1967.
ZEMĚPISNÉ SOUŘADNICE
Polohu jakéhokoliv bodu na zemském povrchu můžeme určit pomocí souřadnicové soustavy.Protože určujeme body na Zemi nazýváme tuto soustavu geocentrickou a její počátek leží ve středu Země.
Tuto soustavu tzv. zeměpisnou síť - tvoří poledníky a rovnoběžky.Osa zemské rotace protíná Zemi v severním a jižním pólu.Průsečnice roviny proložené středem Země kolmo na osu rotace se nazývá rovník.
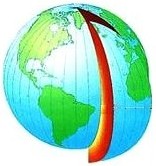
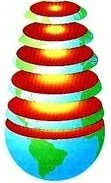
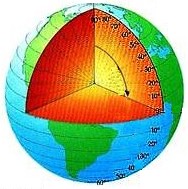
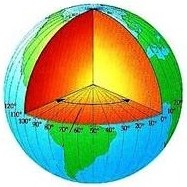
- obrázky znázorňují poledníky,rovnoběžky,zeměpisnou šířku a zeměpisnou délku
poledník - kružnice, která probíhá oběma póly kolmo na rovník.Každým bodem zemského povrchu, mimo pólů, prochází jeden poledník.V praxi se označují poledníky pouze poloviny těchto kružnic.Základní poledník byl zvolen dohodou, nyní je to Greenwichský poledník ( 0).
rovnoběžka - kružnice, která spojuje všechny body se stejnou zeměpisnou šířkou, největší a hlavní rovnoběžka se nazývá rovník.Od rovníků směrem k pólům se rovnoběžky zmenšují.
zeměpisná šířka - úhel, který svírá rovina rovníku a přímka SP.Kdy S je střed Země a P místo ne Zemi jehož zeměpisnou polohu určujeme. Rozlišujeme severní a jižní zeměpisnou šířku. Pro označení zeměpisné šířky se používá řecké písmeno fí a nabývá hodnot od 0 do 90°.
zeměpisná délka - úhel, který svírá rovina základního poledníku a místního poledníku. Rozlišujeme západní a východní zeměpisnou délku. Značí se řeckým písmenem lambda a nabývá hodnot od 0 do 180°
KARTOGRAFICKÁ ZOBRAZENÍ A KARTOGRAFICKÁ PROJEKCE
Protože složitou plochu skutečného zemského povrchu nedokážeme přímo rozvinout do roviny hledal člověk způsoby jak nejpřesněji zemský povrch zachytit na mapě. Výsledkem jsou kartografická zobrazení, které:
- představují způsob, jakým lze obraz zemského povrchu zobrazit do roviny
- určují vztah polohy bodu na zeměkouli nebo na globu k jeho odpovídající poloze na mapě
- kartografická zobrazení jsou přesně definována jejich zobrazovacími matematickými rovnicemi
V případě, že obraz zemského povrchu vznikne geometrickou cestou, přímou projekcí, mluvíme o kartografické projekci.

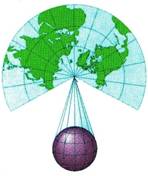
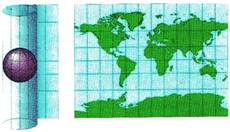
- obrázky znázorňují azimutální,kuželové a válcové zobrazení
- podle zobrazovací plochy (na co se promítá)
- zobrazovací plochou je rovina - vzniká zobrazení azimutální
- zobrazovací plochou je válec - vzniká válcové zobrazení
- zobrazovací plochu tvoří kužel - vzniká kuželové zobrazení
- nepravá zobrazení válcová (pseudocylindrická), kuželová (pseudokónická), azimutální (pseudoazimutální)
- podle polohy zobrazovací osy (podle vzájemné polohy Země a pomocné plochy)
- pólová (normální) - osa kužele nebo válce je totožná s osou zemské rotace nebo se zobrazovací rovina dotýká referenční plochy na jednom pólu
- rovníková (transverzální,příčná) - osa válce nebo kužele leží v rovině rovníku a probíhá jejím středem nebo se zobrazovací rovina dotýká Země na rovníku
- obecná (horizontální,šikmá) - osa válce nebo kužele prochází středem Země, ale nesplývá s osou rotace Země a dotýká se referenční plochy v libovolném bodě mimo pól a rovník
- podle vlastnosti kartografických zkreslení
vzhledem k přibližně kulovému tvaru zem. tělesa je zřejmé, že rovinný obraz zem. povrchu bude vždy obsahovat určité zkreslení - délek,úhlů nebo ploch.
- délkojevné (ekvidistální) zobrazení - nezkresluje délku určitých křivek
- úhlojevné (stejnoúhlé ,konformní) zobrazení - nezkresluje úhly, navigační mapy
- plochojevné (stejnoploché,ekvivalentní) zobrazení - nezkresluje plochy
- vyrovnávací (kompenzační) - zkreslení úhlové i plošné je co nejvíce sníženo, často používané
VOLBA KARTOGRAFICKÉHO ZOBRAZENÍ
Při volbě zobrazení je důležitý účel mapy ale i tvar a rozloha mapovaného území.
Azimutální zobrazení
- projekční plocha se dotýká Země v jednom bodě nebo jej v libovolné vzdálenosti seče.
Rozlišujeme základní polohy zobrazovací roviny - normální,příčnou a obecnou. Rovnoběžky se zobrazí jako soustředné kružnice se středem ve vrcholu kuželové plochy a poledníky tvoří svazek paprsků vycházejících z vrcholu ve stejných úhlových vzdálenostech.
Azimutální zobrazení jsou vhodná pro územítvaru kruhu nebo čtverce.
Azimutální projekce podle umístění bodu promítání
- gnómická projekce - jedná se opromítání ze středu Země na tečnou rovinu, která se jej dotýká v jednom bodě. Rovina promítání se může nacházet v normální, příčné nebo obecné poloze.Rovník leží v nekonečnu a vzdálenosti rovnoběžek se od pólu k rovníku zvětšují.Rovník lze zobrazit.
- stereografická projekce - promítá se z protilehlého bodu promítací roviny umístěného na Zemi. Zobrazovací rovina může být umístěna opět ve všech třech polohách.Vzdálenosti rovnoběžek se směrem od pólů k rovníku mírně zvětšují, lze zobrazit rovník.
- ortografická projekce - bod promítání leží v nekonečnu. Zobrazovací rovina může být umístěna ve všech třech polohách Vzdálenosti rovnoběžek se zmenšují od pólu k rovníku, lze zobrazit rovník.
externí projekce - promítáme z bodu, který se nachází kdekoliv ve vesmíru, neleží na Zemi.Vzdálenosti rovnoběžek se od pólu k rovníku mírně zmenšují.Málo používaná metoda.
Kuželová zobrazení
- projekční plocha se dotýká Země v jednom bodě nebo je ve dvou seče.
Rozlišujeme základní polohy zobrazovací roviny - normální,příčnou a obecnou. Rovnoběžky jsou tvořeny soustřednými kružnicemi se středem v místě dotyku a poledníky tvoří trs paprsků se středem v místě dotyku.
Kuželová zobrazení jsou vhodná pro území tvaru obdélníku, která jsou na glóbu rozložena podél vedlejších kružnic.Kuželové zobrazení se užívá při tvorbě map České republiky.
Válcová zobrazení
- projekční plocha se dotýká v jedné hlavní kružnici nebo je ve dvou seče.
Opět rozlišujeme tři základní polohy zobrazovací roviny - normální,příčnou a obecnou.Rovnoběžky jsou rovnoběžné s rovníkem a jejich rozestupy se liší podle zobrazovací metody.Poledníky jsou přímky kolmé k těmto rovnoběžkám a jejich rozestupy jsou rovnoměrné.
Válcová zobrazení jsou vhodná pro území tvaru obdélníku, které jsou rozloženy podél hlavních nebo sečných kružnic referenční koule.
Nepravá zobrazení
- zobrazují zpravidla stejně rovnoběžky ale poledníky jsou znázorněny jako křivky a polohu jejich jednotlivých bodů získáváme matematickým výpočtem.
Na rozdíl od jednoduchých zobrazení se u nepravých zobrazení tolik neprojevuje délkové zkreslení u rovnoběžek s přibývající zeměpisnou délkou.Nepravá zobrazení se používají na tvorbu map malých měřítek.